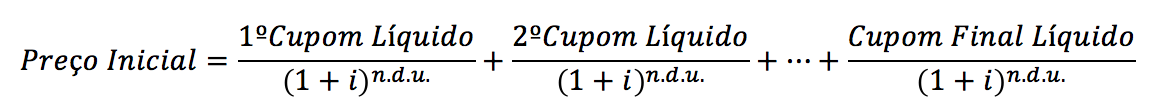Publicidade

Caro Dinheiro

por Samy Dana

Perfil Samy Dana é Ph.D em Business, professor da FGV e escreve no caderno Mercado

Perfil completo

O papel do Sistema Financeiro Nacional

Por Samy
11/06/13 19:10

O Sistema Financeiro Nacional (SFN) é formado por um conjunto de órgãos e instituições, financeiras ou não. Tem como função essencial a promoção do desenvolvimento do País de forma equilibrada, por meio da fiscalização e execução das atividades e operações relacionadas ao crédito e circulação de moeda, bem como por meio da transferência de recursos dos agentes econômicos superavitários para os agentes econômicos deficitários.

É constituído por dois Subsistemas (normativo e de intermediação). O Subsistema Normativo, tratado nesse post, tem como principais instituições componentes o Conselho Monetário Nacional (CMN); o Banco Central do Brasil (BACEN); e a Comissão de Valores Mobiliários (CVM).

O CMN é o órgão máximo do SFN, desempenhando funções estritamente normativas relacionadas à política monetária, creditícia e cambial. Dentre suas principais competências, destacam-se a fixação das diretrizes e normas da política monetária e cambial; a fixação das metas de inflação; a autorização de emissões de papel moeda; a disciplina das operações de crédito e a regulamentação das operações de câmbio, taxas de juros, da constituição e funcionamento das instituições financeiras, bem como do crédito, aplicação dos recursos, operações de redesconto e operações no mercado aberto.

O principal agente executivo das políticas traçadas pelo CMN é o BACEN que é, também, a principal instituição de fiscalização do SFN, tendo como funções disciplinar e fiscalizar o mercado financeiro e executar as políticas monetária, creditícia e cambial.

A CVM, por sua vez, age sob a orientação do CMN no âmbito do mercado de valores mobiliários, e desempenha funções normativas, executivas e fiscalizadoras. Suas principais atribuições são incentivar a poupança no mercado acionário; estimular o funcionamento das bolsas de valores, da bolsa de mercadorias e futuros, e das instituições operadoras do mercado acionário e do mercado de derivativos; assegurar a lisura nas operações de compra/venda de valores mobiliários, e dos contratos de derivativos; promover a expansão dos negócios do mercado acionário e no mercado de derivativos e proteger os investidores do mercado acionário, e do mercado de derivativos.

No próximo post continuaremos com o assunto Sistema Financeiro Nacional, subsistema de intermediação.

Post em parceria com Alex Del Giglio que é graduado em economia pela USP com extensão em finanças pela ESC Bordeaux e mestre em Administração pela FGV. Responsável pela área educacional da Prime Finance Investimentos AAI Ltda com sede em Manaus

Mais opções

Com taxas altas, fundos indexados amargam resultados ruins

Por Samy
10/06/13 07:00

Fundos de ações representam uma alternativa para quem está em busca de novas modalidades de aplicação. Para aqueles que já pensam em aportar capital no mercado de ações mas ainda não sabem como, procurar o auxílio de um gestor pode ser um bom começo.

O fundo de ações caracteriza-se pela participação de um conjunto de investidores com o objetivo de auferir rendimentos a partir da aplicação em uma carteira composta majoritariamente por ações, a qual é definida e gerida por especialistas do mercado financeiro.

O investidor não pode esquecer que aplicar junto a um gestor implica em custos de administração e em alguns casos pode ser cobrada uma taxa de desempenho, a qual estipula uma porcentagem a ser paga caso o rendimento seja maior que determinado patamar.

No caso dos fundos de ações, custos de transação como o de corretagem são diluídos entre diversos investidores e um acompanhamento mais próximo tendem são vantagens frente a investidores individuais. Com isso, o retorno esperado poderá atingir níveis mais elevados.

A escolha do fundo que mais se adequa a suas preferências cabe ao investidor. O mais aconselhável a quem está conhecendo o mercado é aplicar em fundos indexados –ou passivos—, que buscam replicar os rendimentos de determinado índice.

No entanto, o histórico é desanimador, dados da ANBIMA mostram que os fundos indexados obtiveram rendimentos negativos (-15,90%) entre jan/2008 e abril/2013. No mesmo período, a poupança valorizou 44,43%, e o Tesouro Direto, 58,40%.

Par aplicar nesse fundos o investidor paga, invariavelmente, a taxa de administração do fundo, sempre próxima a 2,5%, e pode ter de gastar até 20% do total pelo desempenho, mostrando que não é tão trivial obter retornos significativos neste mercado.

Deve-se sempre levar em conta que o investimento em ações é arriscado. Com uma maior rentabilidade esperada, o investidor deve estar preparado para tomar um risco também maior.

Por isso, por mais sedutor que pareça  investir em fundos de ações , é necessário estar atento às taxa de administração e à reputação do gestor e lembrar que até mesmo quem se dedica há anos a essa prática pode gerar resultados insatisfatórios.

Twitter: @samydana
Mais opções

Mundo Econômico - 09 de Junho

Por Samy
09/06/13 14:30

Panorama Mundo

Os mercados acionários não apresentaram bons retornos durante a semana. Enquanto que as bolsas norte-americanas fecharam com leve alta, mercados europeus e asiáticos apresentaram quedas.

Nos Estados Unidos, dados não mostraram um única tendência e houve destaque para o mercado de trabalho. Na quarta-feira, dados do trabalho no mercado privado vieram abaixo do esperado e derrubaram bolsas. No entanto, o relatório de emprego, divulgado na sexta-feira, mostrou maior criação de empregos e reanimou as bolsas norte-americanas.

Ainda nos EUA, houve a divulgação do Beige Book*. O relatório indicou que a economia americana continua em recuperação moderada, mas que ela deve ganhar força no próximo semestre quando os efeitos do corte de gastos diminuírem.

Na Europa, foi divulgado o PIB do primeiro trimestre da zona de euro que apresentou queda de 0,22%, indicando recessão. Além disso, o PMI* da região aumento de 46,9 para 47,7, porém ainda indica retração.

Na China, PMIs* dos setores industriais e serviços mostraram dados mistos, mas o principal destaque é o discurso do governo que informa que haverá empenho para que a China torne-se um país baseado em demanda interna e para que haja mais importações.

Panorama Brasil

No Brasil, o Ibovespa fechou com queda semanal de 3,53%. Até a quinta-feira, o índice seguiu a tendência dos mercados internacionais, mesmo que acentuando as quedas.

Na sexta-feira, a Standard & Poor’s (S&P) rebaixou a perspectiva de rating do Brasil de “estável” para “negativa”. A notícia derrubou os mercados nacionais e colocou-os na contramão internacional com uma queda diária de 2,39%. A notícia também causou aumento da ponta longa da curva de juros.

Outro destaque foi a desaceleração da inflação, o IPCA teve alta de 0,37% em maio frente a 0,55% em abril. No entanto, o índice acumula, em 12 meses, alta de 6,50%, no teto da meta do Banco Central.

No mercado de câmbio, o dólar apresentou volatilidade maior que a comum e depreciou de R$2,1412 para R$2,1379. Um dos motivos para tanto foi a retirada do IOF para aplicações de estrangeiros em renda fixa local. No entanto, com a informação da S&P, o dólar voltou a ter uma tendência de alta.

Expectativas da Semana

Nessa semana, a volatilidade deve continuar alta no mercado de ações brasileiro.  Haverá divulgação de dados da indústria brasileira, números do varejo e o IBC-Br*. Além disso, haverá vencimento de opções sobre o Ibovespa no dia 17, o que pode aumentar a agitação do mercado.

Ainda há espaço para atenção ao mercado externo. Haverá dados industriais da China e da Europa. Além disso, será divulgado o PIB japonês.

Enquanto isso, o cenário brasileiro deve se manter de inflação alta e juros em alta. Além disso, temos a incerteza cambial, já que o fator que mais afeta o dólar, ainda, é a possibilidade de retirada dos estímulos monetários nos EUA.

*Dicionário Economês-Português

Beige Book– O “Livro Bege” é um relatório publicado oito vezes ao ano pelo FED* que indica o estado da economia do país. A informação apresentada é baseada em dados, pesquisas e entrevistas.

PMI – O Purchasing Managers Index, ou “Índice dos Gestores de Compras”, é um indicador econômico que procura prever a atividade econômica através de pesquisas junto ao setor privado.

IBC-Br (Índice de Atividade Econômica do Banco Central) – Índice calculado pelo Banco Central que tem como objetivo tentar prever o desempenho futuro da economia brasileira.

Post em Parceria com João Lídio Bisneto, graduando em Economia pela FGV-EESP e Presidente da Consultoria Júnior em Economia (CJE) da FGV, em nome da área de pesquisa da empresa.

Mais opções

Trabalhar para pagar impostos

Por Samy
06/06/13 08:22

Até o último dia 30 de maio, segundo o Instituto Brasileiro de Planejamento Tributário, o brasileiro trabalhou apenas para pagar impostos.

Isso porque a média de todos os impostos cobrados do contribuinte brasileiro, imposto de renda, IPTU, IPVA, PIS, Cofins, ICMS, IPI, ISS, contribuições previdenciárias, sindicais, taxas de limpeza pública, coleta de lixo, iluminação pública e emissão de documentos, quando comparada ao salário médio anual, indica que a população trabalha 150 dias apenas para pagar impostos.

 

Comparando com outros valores obtidos no resto do mundo, vê-se, por exemplo, que a Suécia apresenta maior quantidade de dias necessários para pagar todos os impostos. A diferença, nesse caso, consiste no emprego dessa quantia arrecadada.

Estudos do próprio IBPT indicam que o país ocuparia o último lugar como provedor de serviços públicos de qualidade à população, como saúde, educação, segurança, transporte e outros, embora apresenta elevada carga tributária.

Os países que ofereceriam maior retorno à sociedade com a arrecadação tributária seriam, respectivamente, os Estados Unidos, Austrália e Coreia do Sul.

No Brasil, de toda sua renda bruta, o contribuinte terá que utilizar 41,10%, em 2013, para tributação. Essa porcentagem tem aumentado, em 2003, a média foi de 36,98% ; 37,81% em 2004; 38,35% em 2005; 39,72% em 2006; 40,01% em 2007; 40,51% em 2008; 40,15% em 2009; 40,54% em 2010; 40,82% em 2011; e 40,98% em 2012.

Em número de dias de trabalho, vê-se que, historicamente, na década de 70, eram necessários 76 dias  para pagar tributos. Na década de 80, 77 dias e, na década de 90,  102 dias.

Post em Parceria com Giovana Carvalho, graduanda em Economia pela FGV-EESP

Mais opções

Instrumentos Financeiros nº30: Fundos OffShore

Por Samy
05/06/13 07:00

Os fundos offshore são aqueles constituídos fora do território brasileiro, mas cujo gestor localiza-se no Brasil. Por meio desse instrumento, é possível investir em títulos estrangeiros como os do tesouro norte-americano, em ações de companhias europeias, asiáticas, norte-americanas e, também, brasileiras negociadas lá fora.

Investir no exterior, ao contrário do que muitos pensam, não é ilegal e esse veículo é um passaporte.

Assim como os demais fundos, os Offshore são constituídos como uma comunhão de recursos financeiros sob a forma de condomínio. A principal diferença está no objetivo dos investidores que é, neste caso, a aplicação de recursos com remuneração referenciada no risco Brasil, Norte-Americano ou Europeu.

Essas aplicações são sediadas, geralmente, em paraísos fiscais e investem em ativos pelo mundo afora. Diversas instituições brasileiras possuem expertise na constituição de fundos offshore.

Os investidores que aplicam nesses fundos se tornam proprietários de uma fração do fundo e são denominados de cotistas.  A maior parte dos fundos exige um aporte de no mínimo US$ 50 mil, o equivalente a cerca de R$ 100 mil, para iniciar os investimentos. Desta forma, são fundos destinados a médios e grandes investidores, normalmente, qualificados.

Antes de decidir por um fundo offshore, é interessante pesquisar as rentabilidades históricas, a série histórica das taxas de câmbio, a reputação do gestor e o perfil dos produtos de investimento que compõem a carteira do fundo.

Esses fundos são recomendados para diversificação dos investimentos. Entretanto, é importante estar ciente que o recurso estará investido em outra moeda que não o real, sendo assim o investimento correrá, além do risco da aplicação, o risco cambial.

Uma das principais diferenças de optar por esses fundos é a não relação do fundo com a legislação brasileira. Esses fundos estão submetidos, apenas, às regras de câmbio do Banco Central do Brasil (BACEN). Uma delas é a Resolução 3.250/2004.

Os  custos com a aplicação nesses fundos são elevados e por vezes não compensam a diversificação do investimento. Há o valor da custódia exercida por um banco no exterior que detém os papéis do investidor, bem como todos os custos administrativos.

Entre as vantagens oferecidas pelos fundos de investimento offshore aos investidores podem-se destacar: a comodidade de ter investimentos geridos por profissionais especialistas; a redução de risco por meio de um processo de diversificação internacional da carteira; e a transparência.

Em relação à tributação, existem alguns benefícios fiscais dependendo do local onde os recursos estão investidos. Portanto, vale a pena obter junto ao gestor informações detalhadas quanto aos aspectos fiscais.

É possível acompanhar o mercado de fundos offshore por meio de revistas, jornais e sites especializados ou ainda contar com assessoria de profissionais de investimentos.

Bons investimentos!

Post em parceria com Alex Del Giglio que é graduado em economia pela USP com extensão em finanças pela ESC Bordeaux e mestre em Administração pela FGV. Responsável pela área educacional da Prime Finance Investimentos AAI Ltda com sede em Manaus.

Mais opções

Instrumentos financeiros nº29: Cédulas de Debêntures (CDs)

Por Samy
04/06/13 07:00

As Cédulas de Debêntures (CDs) são instrumentos financeiros que podem ser emitidos por bancos comerciais, bancos de investimento, bancos de desenvolvimento e bancos múltiplos com carteira comercial, de investimento ou de desenvolvimento.

Na prática, funcionam como um empréstimo que o investidor faz a um banco em troca de uma remuneração.

Para o banco, essa é uma forma de captação a partir da securitização de debêntures emitidas por empresas não financeiras de capital aberto. Deste modo, permitem que o banco subscreva debêntures de empresas e, em seguida, emita CDs para obter recursos.

O risco de aplicação nas CDs pode ser considerado baixo em bancos que contam com boa reputação e alta solidez. O investidor só perderá os recursos aplicados, caso o banco vá à falência. Apesar das CDs estarem ligadas às debêntures de empresas, o risco do investidor se resume ao banco.

Uma característica importante é que as CDs são papéis de médio/longo prazo. O prazo mínimo de vencimento é de 60 dias contados da data de emissão e o prazo máximo de vencimento equivale ao vencimento das debêntures que lhes deram origem. Esse prazo pode ser explicado pelo fato de que as empresas emissoras das debêntures utilizam os recursos em investimentos que demoram, em regra, anos para se realizarem por completo.

Como possuem prazos de vencimento mais dilatados, comparativamente aos instrumentos de captação tradicionais como a Poupança e os CDBs, permitem ao banco um funding de prazo mais longo.

Sob o ponto de vista dos investidores, apesar da menor liquidez, apresentam remuneração mais atraente e se constituem em uma modalidade de investimento democrática, destinada a pequenos, médios e grandes investidores. É comum encontrar aplicações mínimas que iniciam com menos de R$ 500,00.

O investidor ao comprar esse título deve atentar, especialmente, ao prazo de vencimento, ao rating de crédito das debêntures que compõem as cédulas e ao rating de crédito do banco emissor. Vale observar que as CDs são consideradas títulos de dívidas securitizadas em debêntures.

Em relação à tributação, as CDs sofrem incidência de imposto de renda (IR) regressivo sobre os rendimentos auferidos. A alíquota de IR é de 22,5% para operações com prazo de até 180 dias, 20% para operações de 181 dias até 360 dias, 17,5% para operações de 361 dias até 720 dias e 15% para operações de prazo superior a 720 dias. O  imposto de renda é retido na fonte por ocasião do recebimento dos rendimentos.

Para investir em CDs, é preciso ser cliente de um banco que negocie esse produto. Como é um papel pouco negociado no mercado financeiro, não há muita informação disponível em revistas, jornais e sites especializados. Desta forma, para investir nessas cédulas é importante contar com assessoria de profissionais de investimentos.

Bons investimentos!

Post em parceria com Alex Del Giglio que é graduado em economia pela USP com extensão em finanças pela ESC Bordeaux e mestre em Administração pela FGV. Responsável pela área educacional da Prime Finance Investimentos AAI Ltda com sede em Manaus.

Mais opções

Brasileiro paga caro com cosméticos

Por Samy
03/06/13 07:00

O povo brasileiro já se encontra entre os principais consumidores de produtos de beleza do mundo, ocupando atualmente a terceira posição no ranking, ficando atrás apenas de Estados Unidos e Japão.

Feiras e exposições já passaram a fazer parte do calendário nacional de eventos, e inovações do mundo inteiro chegam a terras tupiniquins com propostas cada vez mais mirabolantes que prometem milagres e fórmulas de rejuvenescimento.

O efeito geral é positivo, pois cria-se uma abertura para investimentos em um novo mercado no país, e permite-se que novas tecnologias sejam exploradas internamente, favorecendo o produtor nacional.

Em números, o fenômeno impressiona. Somente no ano de 2012, a indústria nacional faturou R$34 bilhões líquidos, e a expectativa para 2013 é ainda maior. A quantidade de salões de beleza e lojas de cosméticos não pára de aumentar, e a geração de emprego mais do que dobrou nos últimos dez anos.

Muito desse movimento se deve ao recente aumento da renda das famílias brasileiras. As classes B, C e D gastam, respectivamente R$281, R$236,5 e R$208,9 milhões mensais com produtos do gênero, sendo as principais responsáveis pela expansão do mercado.

Economicamente falando, o crescimento é belíssimo. Mas e o impacto sobre as finanças pessoais, como fica?

Segundo dados divulgados pela consultoria GS&MD – Gouvêa de Souza, o brasileiro gastou, em média, R$112,00 por mês no ano de 2012 com produtos de beleza a higiene pessoal. O valor pode não parecer absurdamente elevado, mas a aquisição contínua pode se tornar um costume, e criar um peso para as contas da família.

Além disso, é importante considerar que os produtos vendidos no Brasil não são nada baratos se comparados a valores externos, e o brasileiro, mesmo que não-intencionalmente, acaba sempre optando pelo mais caro.

Não se pode negar, de forma alguma, que há grande satisfação em sentir-se bem consigo mesmo. Contudo, não se pode deixar que gastos aparentemente inofensivos, como a compra de um esmalte novo ou um creme de barbear refrescante, deteriorem o orçamento pessoal, afinal, não é só de beleza que vive o homem.

Mais opções

Mundo Econômico - 02 de Junho

Por Samy
02/06/13 11:00

Panorama Mundo

Na semana passada, as principais bolsas mundiais não apresentaram tendência e fecharam o período em queda.

Nos Estados Unidos, notícias boas não mais, necessariamente, causam altas no mercado. Como uma economia forte pode indicar redução dos estímulos monetários, dados positivos e negativos começam a apresentar consequências ambíguas.

Mesmo coma semana apresentando dados positivos, como o PMI* de Chicago, que ficou em 58,7, ante expectativas de 49,3, as bolsas norte-americanas apresentaram quedas semanais.

Na Europa, a reforma do pensamento político continua. A União Europeia (UE) admitiu que austeridade não trará saída para a crise, permitindo que três das cinco maiores economias da região (França, Espanha e Holanda) estourem o limite de déficit orçamentário, sob a condição de reformas no mercado de trabalho.

Enquanto isso, na Alemanha, o número de pedidos de seguro-desemprego aumentou em 21 mil em maio na comparação com abril, em termos sazonalmente ajustados. O resultado veio bem acima da previsão de analistas, que era de alta de 3 mil pedidos.

Na Ásia, foi divulgado o Índice dos Gerentes de Compras (PMI) da indústria chinesa. O indicador ficou em 50,8 em maio (contra 50,6 em abril), superando as expectativas do mercado. O FMI ainda reduziu a previsão de crescimento da China em 2013 de 8% para 7,75%.

Na Índia, o elevado déficit de 7% do PIB na conta corrente começa a preocupar, como deixou claro o presidente do banco central do país.

Panorama Brasil

No Brasil, o Ibovespa amargou uma queda semanal de 5,14%, puxado pelo desempenho ruim das blue chips*.

Outro motivo para a queda da bolsa foi o crescimento do PIB brasileiro de 0,6% no primeiro trimestre. A expectativa era de 0,9%.

Com a economia mostrando desempenho abaixo do esperado, o mercado rebaixou suas previsões para a alta da SELIC: começaram a ver uma alta de 0,25 p.p ao invés de 0,50p.p. No entanto, o Banco Central surpreendeu o mercado e colocou a SELIC no patamar de 8% a.a., com uma elevação de 0,50%, o que também ajudou na queda da bolsa. Assim, a curva de juros teve movimentações bruscas na semana com uma alta generalizada no total.

Quanto à inflação, com poucas novidades, o IPC-Fipe mostrou que a inflação na cidade de São Paulo continua no mesmo patamar: alta de 0,18% na terceira quadrissemana de maio.

Por fim, o mercado de moedas trouxe surpresas. O dólar apresentou uma alta expressiva na semana, saindo de R$2,0525 na sexta-feira, dia 24, para R$2,1424 na última sexta-feira. O dado ruim do PIB aliado a expectativas de retirada dos estímulos monetários nos EUA foi o principal responsável por essa movimentação. Nem a alta acima do esperado da SELIC nem a intervenção do BC na sexta-feira foram capazes de frear a moeda norte-americana.

Expectativas da Semana

Agora, com os investidores estrangeiros incapazes de definir o ideal (dados positivos ou negativos nos EUA), o ato de prever resultados torna-se mais difícil. O que se pode afirmar é que se inicia um período de algumas semanas em que os mercados tenderão a andar lateralmente, talvez, com um viés de baixa.

No Brasil, os investidores, que já não se apresentavam otimistas, devem levar o Ibovespa a ter, novamente, resultados ruins.

Para a próxima semana, especificamente, deverá se basear em informações advindas do FED*. Haverá quatro discursos de diretores e a instituição divulgará o Beige Book*. Também serão divulgados PMIs* da Europa e da China.

No Brasil, destaque para a inflação, com o anúncio do IPCA de maio, e para a ata do Copom. Além disso, investidores ficarão atentos às novas movimentações do câmbio. O dólar deve apresentar maior volatilidade na semana e intervenções do BC são esperadas, pois a entidade já indicou que sua preocupação é a volatilidade desse mercado.

*Dicionário Economês-Português

PMI – O Purchasing Managers Index, ou “Índice dos Gestores de Compras”, é um indicador econômico que procura prever a atividade econômica através de pesquisas junto ao setor privado.

Blue chips – É o termo empregado nos mercados de ações para designar ações de empresas de empresas de alto valor de mercado e/ou bem estabelecidas com comprovada lucratividade. No caso brasileiro, o termo refere-se, principalmente, à Petrobrás e à Vale.

FED (Federal Reserve) – Banco Central norte-americano.

Beige Book – O “Livro Bege” é um relatório publicado oito vezes ao ano pelo FED* que indica o estado da economia do país. A informação apresentada é baseada em dados, pesquisas e entrevistas.

Post em Parceria com João Lídio Bisneto, graduando em Economia pela FGV-EESP e Presidente da Consultoria Júnior em Economia (CJE) da FGV, em nome da área de pesquisa da empresa.

Mais opções

Saiba como o título pós-fixado NTN-B funciona, parte 8

Por Samy
01/06/13 01:53

Para finalizar a série Em Busca do Tesouro Direto, daremos sequência às Notas do Tesouro Nacional, série B, abordando agora a relação entre preço e taxa/rentabilidade.

Assim como nos demais títulos, o investidor pode estipular uma rentabilidade de interesse e,a  partir desta taxa, identificar qual o preço máximo que deve ser pago pelo título.

Para isso, vamos supor a compra de uma NTNB 150820, ou seja, um título de NTN-B com vencimento em 15/08/2020.

Supondo que este título foi comprado em 27/05/2013 por R$ 2.594,64, ou seja, possuía uma taxa de compra de 4,09% anual. Vale lembrar que a NTN-B é um título indexado à inflação, ou seja, neste caso o investidor receberá os 4,09% além da variação do IPCA no período.

Para facilitar o entendimento do tema deste post, vamos dividi-lo em dois cenários.

O primeiro, supondo que não haja inflação (ou seja, IPCA = 0%) durante o período da aplicação. Já no segundo, que há uma inflação constante de 5% ao ano.

  • Cenário A: IPCA = 0%

Suponha que o investidor queira uma rentabilidade bruta de 12% ao ano sobre o título NTN-B. Diante disso, qual deveria ser o preço do título para que ele tenha essa rentabilidade desejada?

Para iniciar estes cálculos, deve-se primeiramente encontrar qual será a rentabilidade bruta por dia útil da aplicação. Para isso, basta utilizar a fórmula:

A “taxa anual” representa a rentabilidade bruta de interesse. Já o “1/252” é o conversor que transformará a taxa anual em uma taxa ao dia útil, já que em um ano há 252 dias úteis.

Ou seja, a cada dia útil, o investidor deseja uma valorização de aproximadamente 0,045% no título. Em finanças essa taxa é chamada de Taxa Interna de Retorno. Caso tenha dificuldades com este termo, basta acessar este post em que já fizemos algumas explicações sobre.

Como a NTN-B é um título pós fixado e que oferece ao investidor o pagamento de cupons semestrais, devemos encontrar o valor na data de compra, conhecido também como valor presente do título.

Para entender a questão do valor presente, basta ver este post já publicado.

Com isso, o investidor deve realizar a seguinte fórmula:

O “i” indica a taxa desejada que, conforme já calculamos, representa o valor de 0,04498% ao dia útil. O termo “n.d.u.” é o número de dias úteis que houveram entre a data de compra até seu respectivo Cupom Bruto.

Por exemplo, de acordo com a calculadora, até o 1º Cupom Bruto foram 56 dias úteis. Até o 2º Cupom, 184 dias úteis.

Não esqueça que para calcular o valor de cada Cupom Bruto é necessário identificar o VNA (Valor Nominal Atualizado) na data de compra, que neste caso é dia 27/05/2013.

Como a data de compra não é dia 15, conforme explicamos anteriormente, o Valor Nominal Atualizado precisa ser estimado. Uma das formas mais simples é pelo site da ANBIMA.

De acordo com a ANBIMA,  no dia 27/05/2013, data de compra do título, o VNA era de R$ 2.290,15. O VNA é atualizado diariamente com a variação do IPCA. No entanto, como o cenário A o IPCA é 0%, o valor do VNA que é de R$ 2.290,15 se manterá o mesmo durante toda aplicação.

Com o VNA em mãos, fica fácil encontrar o valor dos cupons brutos. Como a NTN-B possui taxa de juros de 6% ao ano e os cupons são pagos semestralmente, devemos converter esta taxa anual em uma semestral. Veja:

De posse da taxa semestral, basta seguir com os cálculos do Cupom Bruto:

Ou seja, supondo que não haja inflação no período da aplicação, cada Cupom Bruto Semestral será de R$ 67,70.

Agora para o Cupom Bruto Final, basta aplicar a fórmula:

De posse dos dados necessários, retomamos à fórmula do cálculo do valor presente. Veja:

Ou seja, caso o investidor queira uma rentabilidade bruta de 12% ao ano, o preço máximo que deve pagar no título é de R$ 1.699,50.

Agora, supondo ainda o cenário com inflação à 0%, entenda como realizar os cálculos caso o investidor queira uma rentabilidade líquida de 12% ao ano.

Novamente, é necessário transformar a taxa anual em uma taxa por dias úteis. Sabemos que 12% ao ano equivale à uma taxa de 0,04498% ao dia útil.

De posse da taxa, para encontrar o preço máximo para que o título tenha a rentabilidade desejada, basta seguir com a fórmula:

Agora é necessário encontrar então o valor de cada Cupom Líquido, ou seja, descontar do cupom bruto as taxas de administração e custodia, além do imposto de renda.

Os cálculos necessários para encontrar os Cupons Líquidos foram demonstrados no post, onde ensinamos a calcular no modo “papel e caneta”.

Pela nossa calculadora o investidor encontra os valores facilmente, basta inserir os dados solicitados e ela retorna com o valor de cada Cupom Líquido.

De acordo com a calculadora, o valor do 1º Cupom Líquido é de R$ 59,55. O 2º Cupom Líquido, R$ 50,24. O 3º, R$ 49,26. Até o último, no valor de R$ 2382,02.

Com os dados em mãos, basta jogá-los na fórmula:

Realizando os cálculos, encontramos:

Entretanto, como estamos falando de rentabilidade líquida, devemos ainda considerar o custo que o investidor teve ao adquirir o título, ou seja, a taxa de administração na entrada.

Para isso, é necessário descontar ainda esta taxa. Entenda:

Supondo uma taxa de administração de 0,5%, vem:

Ou seja, caso o investidor adquira um título deste por R$ 1519,11, ele garantirá uma rentabilidade líquida de 12% ao ano. Caso pague mais que estes 1519,11, irá se deparar com uma rentabilidade menor.

  •  Cenário B: IPCA = 5%

Agora, supondo então um cenário em que há uma inflação constante de 5% ao ano, seguimos com os cálculos.

Novamente, imagine que o investidor queira uma rentabilidade bruta anual de 12% acima da inflação, que neste caso é de 5%.

Para encontrar a taxa requerida, segue a fórmula:

Ou seja, o investidor requer uma taxa de 0,06435% ao dia útil.

Para encontrar o preço, o cálculo é basicamente o mesmo:

Porém, os Cupons Brutos agora não serão uniformes. Como o VNA será atualizado diariamente desta vez (IPCA de 5% ao ano), cada Cupom Bruto seguirá esta evolução do VNA.

Neste post ensinamos como encontrar o valor de cada Cupom Bruto de acordo com a trajetória do VNA.

Pela nossa calculadora o investidor tem acesso a cada um destes valores, o que facilita os cálculos. Segundo ela, o 1º Cupom Bruto, para uma inflação anual de 5%, é de R$ 68,40. O 2º Cupom é de R$ 70,11. Até que o Cupom Final Bruto é de R$ 3352,95.

De posse dos dados, basta seguir com os cálculos:

Sendo assim, pagando R$ 1.778,11 e assumindo que o IPCA se mantenha à 5% ao ano durante toda aplicação do título, o investidor garante uma rentabilidade bruta de 12% ao ano acima da variação do IPCA, que neste caso é 5%.

E, para finalizar, supondo agora que o investidor almeje uma rentabilidade líquida de 12% ao ano.

Como já visto, os 12% ao ano equivalem à  0,06435% ao dia útil.

E, novamente, a fórmula do preço quando tratamos da rentabilidade líquida:

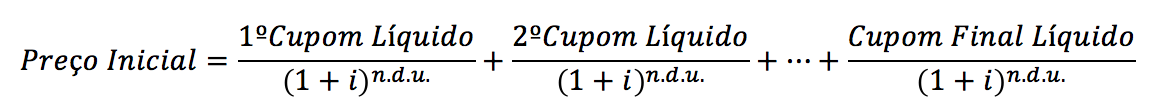
Já que estamos abordando um cenário com presença de uma inflação de 5% ao ano, há variação no Valor Nominal Atualizado (VNA).

E como há alteração no VNA com o passar dos dias úteis, há consequente alteração no valor dos Cupons Líquidos.

Neste post mostramos como realizar este cálculo especificamente, caso o leitor queira entender melhor.

Por meio de nossa calculadora o investidor encontra facilmente os valores de cada Cupom Líquido, já atualizado pelo VNA.

Segundo ela, o 1º Cupom Líquido equivale a R$ 60,16. O 2º, a R$ 52,02. Até que o último, o Cupom Líquido Final, vale R$ 3224,49.

Assim, é possível dar sequência aos cálculos:

Efetuando o cálculo completo, encontra-se então o seguinte Preço Inicial:

E, como último detalhe, devemos descontar a taxa de administração do Preço Inicial encontrado.

Supondo a mesma taxa de administração do primeiro cenário, ou seja, de 0,5%, vem:

Desta forma, para que o investidor garanta uma rentabilidade líquida de 12% ao ano, dois fatos devem ocorrer:

  • O IPCA deve-se manter inalterado em 5% ao ano durante todo o tempo da aplicação, ou seja, entre a data de compra e a de vencimento.
  • O preço do título deve ser de R$ 1.532,19.

É por estes motivos que a chance de se acertar com exatidão a rentabilidade nominal a receber de um título pós-fixado é bem difícil, no entanto, o investidor, no caso da NTN-B e NTN-B Principal, consegue prever a rentabilidade real, ou seja, acima da inflação.

Artigo em parceria com Miguel Longuini, graduando em Administração de Empresas pela FGV-EAESP e Diretor Administrativo/Financeiro da Consultoria Júnior de Economia (CJE) da FGV.

Mais opções

Aumento da Selic pode não surtir o efeito

Por Samy
31/05/13 10:22

Em anúncio na última quarta, o Comitê de Política Monetária decidiu aumentar a taxa de juros básica da economia, a Selic em 0,5% para 8% ao ano. Tal taxa entrou em vigor na quinta e permanece assim até o próximo dia 10 de julho.

Com esse valor, a taxa se equipara ao patamar que apresentava de julho a agosto do ano passado.

Desse modo, o Banco Central sinaliza preferência por manter o controle da inflação ainda que um pouco à revelia do crescimento do produto nacional.

A alta inflação já daria sinais negativos sobre a renda disponível e o consumo das famílias, que cresceu apenas 0,1% no primeiro trimestre desse ano.

A atitude do BC se mostrou surpreendente para muitos analistas no mercado, que, embora apostassem em alta da taxa de juros, acreditavam que o aumento seria de apenas 0,25%.

Tal expectativa se deveu ao fato de que, na manhã de ontem, o IBGE divulgou dados relativos ao PIB e o crescimento de 0,6% do primeiro trimestre em relação ao mesmo período de 2012 decepcionou até mesmo o governo, que esperava crescimento de 1% e o mercado, que esperava alta de 0,9%.

No mesmo dia, os Estados Unidos divulgaram seus dados relativos ao produto, evidenciando alta de 2,4% em relação ao primeiro trimestre de 2012, o que torna a comparação internacional do Brasil ainda pior.

Acredita-se que o problema principal que afeta o crescimento nacional seja ocasionado pela oferta e não pela demanda.

Assim, é antes necessário estimular investimentos e melhorar a infraestrutura brasileira do que estimular a demanda.

É, de certa forma, um erro considerar que esse aumento na Selic prejudica os investimentos. Isso porque o crédito oferecido no país apresenta um spread tão vultoso que a diferença marginal com essa alta é quase desprezível.

Novamente, a lição aprendida é que sem aumento na oferta correspondente ao incremento de demanda , o único efeito observado na e economia será a inflação e medidas como a elevação da Selic serão necessárias.

Post em Parceria com Giovana Carvalho, graduanda em Economia pela FGV-EESP

Mais opções
Publicidade
Publicidade
Publicidade
Publicidade
Publicidade